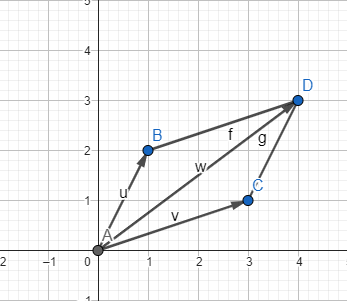
Linear Algebra Vector What is a vector? A vector magnitude direction Vectors added together multiplied by scalars
a, Example of Vector
b, Example of Added Vector
c, Example of Scale Vector
Vector Representation Only 2D and 3D can use geometric vectors . How many extra dimensions would the vector have?
In n-dimensional space, the vectors will be represented as follows:
a = [ a 1 a 2 a 3 . . . a n ] ∈ R n , v = [ 1 2 3 ] ∈ R 3 a= \begin{bmatrix} a_1\\a_2\\a_3\\...\\a_n \end{bmatrix} \in R^n , v= \begin{bmatrix} 1\\2\\3 \end{bmatrix} \in R^3 a = ⎣ ⎡ a 1 a 2 a 3 ... a n ⎦ ⎤ ∈ R n , v = ⎣ ⎡ 1 2 3 ⎦ ⎤ ∈ R 3 In multidimensional space vectors also have two properties: addition and multiplication
[ a 1 a 2 . . . a n ] + [ b 1 b 2 . . . b n ] = [ a 1 + b 1 a 2 + b 2 . . a n + b n ] , α ∗ [ a 1 a 2 . . . a n ] = [ α ∗ a 1 α ∗ a 2 . . . α ∗ a n ] \begin{bmatrix} a_1\\a_2\\...\\a_n \end{bmatrix} + \begin{bmatrix} b_1\\b_2\\...\\b_n \end{bmatrix} = \begin{bmatrix} a_1+b_1\\a_2+b_2\\..\\a_n +b_n \end{bmatrix}, \quad \alpha * \begin{bmatrix} a_1\\a_2\\...\\a_n \end{bmatrix} =\begin{bmatrix} \alpha *a_1\\\alpha *a_2\\...\\\alpha *a_n \end{bmatrix} ⎣ ⎡ a 1 a 2 ... a n ⎦ ⎤ + ⎣ ⎡ b 1 b 2 ... b n ⎦ ⎤ = ⎣ ⎡ a 1 + b 1 a 2 + b 2 .. a n + b n ⎦ ⎤ , α ∗ ⎣ ⎡ a 1 a 2 ... a n ⎦ ⎤ = ⎣ ⎡ α ∗ a 1 α ∗ a 2 ... α ∗ a n ⎦ ⎤ Matrix What is the matrix? Matrix a set of numbers arranged in rows and columns so as to form a rectangular array .
Example of matrix
A = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 . . . a m n ] ∈ R m × n = c o n c a t ( [ a 11 a 12 . . . a 1 n ] , [ a 21 a 22 . . . a 2 n ] , . . . , [ a n 1 a n 2 . . . a m n ] ) A = \begin{bmatrix} a_{11}&a_{12}&...&a_{1n}\\ a_{21}&a_{22}&...&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&...&a_{mn} \end{bmatrix} \in R^{m\times{}n}\\ \\ = concat( \begin{bmatrix} a_{11}\\a_{12}\\...\\a_{1n} \end{bmatrix}, \begin{bmatrix} a_{21}\\a_{22}\\...\\a_{2n} \end{bmatrix}, ..., \begin{bmatrix} a_{n1}\\a_{n2}\\...\\a_{mn} \end{bmatrix}) A = ⎣ ⎡ a 11 a 21 ⋮ a m 1 a 12 a 22 ⋮ a m 2 ... ... ⋱ ... a 1 n a 2 n ⋮ a mn ⎦ ⎤ ∈ R m × n = co n c a t ( ⎣ ⎡ a 11 a 12 ... a 1 n ⎦ ⎤ , ⎣ ⎡ a 21 a 22 ... a 2 n ⎦ ⎤ , ... , ⎣ ⎡ a n 1 a n 2 ... a mn ⎦ ⎤ ) Matrix addition A ∈ R m × n , B ∈ R m × n A + B = [ a 11 + b 11 a 12 + b 21 . . . a 1 n + b 1 n a 21 + b 21 a 22 + b 22 . . . a 2 n + b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 + b m 1 a m 2 + b m 2 . . . a m n + b m n ] ∈ R m × n A \in R^{m\times{}n},\quad B \in R^{m\times{}n} \\ A+B= \begin{bmatrix} a_{11}+b_{11}&a_{12}+b_{21}&...&a_{1n}+b_{1n}\\ a_{21}+b_{21}&a_{22}+b_{22}&...&a_{2n}+b_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}+b_{m1}&a_{m2}+b_{m2}&...&a_{mn}+b_{mn} \end{bmatrix} \in R^{m\times{}n} A ∈ R m × n , B ∈ R m × n A + B = ⎣ ⎡ a 11 + b 11 a 21 + b 21 ⋮ a m 1 + b m 1 a 12 + b 21 a 22 + b 22 ⋮ a m 2 + b m 2 ... ... ⋱ ... a 1 n + b 1 n a 2 n + b 2 n ⋮ a mn + b mn ⎦ ⎤ ∈ R m × n Hadamard product A ∈ R m ∗ n , B ∈ R m ∗ n A ⨂ B = [ a 11 b 11 a 12 b 21 . . . a 1 n b 1 n a 21 b 21 a 22 b 22 . . . a 2 n b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 b m 1 a m 2 b m 2 . . . a m n b m n ] ∈ R m ∗ n A \in R^{m*n},\quad B \in R^{m*n} \\ A \bigotimes B= \begin{bmatrix} a_{11}b_{11}&a_{12}b_{21}&...&a_{1n}b_{1n}\\ a_{21}b_{21}&a_{22}b_{22}&...&a_{2n}b_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}b_{m1}&a_{m2}b_{m2}&...&a_{mn}b_{mn} \end{bmatrix} \in R^{m*n} A ∈ R m ∗ n , B ∈ R m ∗ n A ⨂ B = ⎣ ⎡ a 11 b 11 a 21 b 21 ⋮ a m 1 b m 1 a 12 b 21 a 22 b 22 ⋮ a m 2 b m 2 ... ... ⋱ ... a 1 n b 1 n a 2 n b 2 n ⋮ a mn b mn ⎦ ⎤ ∈ R m ∗ n Matrix multiplication A ∈ R m × n , B ∈ R n × k , C = A B , C i j = ∑ k = 1 n a i k b k j [ 1 2 2 0 1 1 ] [ 2 3 ] = [ 1 × 2 + 2 × 3 2 × 2 + 0 × 3 1 × 2 + 1 × 3 ] = [ 8 4 5 ] A \in R^{m\times{}n},\quad B \in R^{n\times{}k}, \quad C =AB, \quad C_{ij} = \sum^n_{k=1} a_{ik}b_{kj} \\ \begin{bmatrix} 1&2\\2&0\\1&1 \end{bmatrix} \begin{bmatrix} 2\\3 \end{bmatrix} =\begin{bmatrix} 1\times{}2+2\times{}3\\2\times{}2+0\times{}3\\1\times{}2+1\times{}3 \end{bmatrix} = \begin{bmatrix} 8\\4\\5 \end{bmatrix} A ∈ R m × n , B ∈ R n × k , C = A B , C ij = k = 1 ∑ n a ik b kj ⎣ ⎡ 1 2 1 2 0 1 ⎦ ⎤ [ 2 3 ] = ⎣ ⎡ 1 × 2 + 2 × 3 2 × 2 + 0 × 3 1 × 2 + 1 × 3 ⎦ ⎤ = ⎣ ⎡ 8 4 5 ⎦ ⎤ Different view
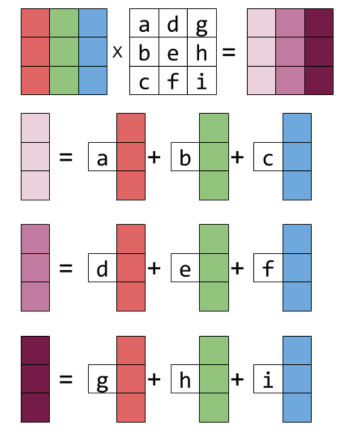
Example
[ 1 2 2 0 1 1 ] [ 2 3 ] = 2 [ 1 2 1 ] + 3 [ 2 0 1 ] = [ 8 4 5 ] \begin{bmatrix} 1&2\\2&0\\1&1 \end{bmatrix} \begin{bmatrix} 2\\3 \end{bmatrix} =2 \begin{bmatrix} 1\\2\\1 \end{bmatrix} + 3 \begin{bmatrix} 2\\0\\1 \end{bmatrix} = \begin{bmatrix} 8\\4\\5 \end{bmatrix} ⎣ ⎡ 1 2 1 2 0 1 ⎦ ⎤ [ 2 3 ] = 2 ⎣ ⎡ 1 2 1 ⎦ ⎤ + 3 ⎣ ⎡ 2 0 1 ⎦ ⎤ = ⎣ ⎡ 8 4 5 ⎦ ⎤ Identity matrix Identity matrix is a square matrix, with the value:
I i j = { 1 if i = j 0 if i ≠ j I_{ij} = \begin{cases} 1 &\quad \text{if } i=j \\ 0 &\quad \text{if } i \neq j \end{cases} I ij = { 1 0 if i = j if i = j I n = [ 1 0 ⋯ 0 0 1 ⋯ 0 ⋯ ⋯ ⋯ ⋯ 0 0 ⋯ 1 ] ∈ R n × n I_n= \begin{bmatrix} 1&0&\cdots&0\\ 0&1&\cdots&0\\ \cdots&\cdots&\cdots&\cdots\\ 0&0&\cdots&1 \end{bmatrix} \in R^{n\times n} I n = ⎣ ⎡ 1 0 ⋯ 0 0 1 ⋯ 0 ⋯ ⋯ ⋯ ⋯ 0 0 ⋯ 1 ⎦ ⎤ ∈ R n × n Matrix properties ∀ A ∈ R m × n , B ∈ R n × p , C ∈ R p × q : ( A B ) C = A ( B C ) \forall A \in R^{m\times n}, B \in R^{n\times p}, C \in R^{p\times q}: (AB)C = A(BC) ∀ A ∈ R m × n , B ∈ R n × p , C ∈ R p × q : ( A B ) C = A ( BC ) ∀ A , B ∈ R m × n , C , D ∈ R n × p \forall A, B \in R^{m\times n}, C, D \in R^{n\times p} \\ ∀ A , B ∈ R m × n , C , D ∈ R n × p ( A + B ) C = A C + B C A ( C + D ) = A C + A D \quad \quad \quad (A+B)C=AC + BC \\ \quad \quad \quad A(C+D)=AC + AD ( A + B ) C = A C + BC A ( C + D ) = A C + A D ∀ A ∈ R m × n : I m A = A I n = A , note that : I m ≠ I n \forall A \in R^{m \times n}: I_mA = AI_n =A, \text{note that }: I_m \neq I_n ∀ A ∈ R m × n : I m A = A I n = A , note that : I m = I n Transpose A ∈ R m × n ⇒ B = A T ∈ R n × m , a i j = b j i A \in R^{m\times n} \Rightarrow B = A^T \in R^{n \times m}, a_{ij} = b_{ji} A ∈ R m × n ⇒ B = A T ∈ R n × m , a ij = b ji A = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 . . . a m n ] ⇒ B = [ a 11 a 21 . . . a m 1 a 12 a 22 . . . a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n . . . a m n ] A = \begin{bmatrix} a_{11}&a_{12}&...&a_{1n}\\ a_{21}&a_{22}&...&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&...&a_{mn} \end{bmatrix} \Rightarrow B = \begin{bmatrix} a_{11}&a_{21}&...&a_{m1}\\ a_{12}&a_{22}&...&a_{m2}\\ \vdots&\vdots&\ddots&\vdots\\ a_{1n}&a_{2n}&...&a_{mn} \end{bmatrix} A = ⎣ ⎡ a 11 a 21 ⋮ a m 1 a 12 a 22 ⋮ a m 2 ... ... ⋱ ... a 1 n a 2 n ⋮ a mn ⎦ ⎤ ⇒ B = ⎣ ⎡ a 11 a 12 ⋮ a 1 n a 21 a 22 ⋮ a 2 n ... ... ⋱ ... a m 1 a m 2 ⋮ a mn ⎦ ⎤ A matrix A ∈ R m × n is symmetric if A T = A \text{A matrix } A \in R^{m\times n} \text{is symmetric if } A^T = A A matrix A ∈ R m × n is symmetric if A T = A Inverse Square matrix A and matrix B belong to the same n-dimensional space with the property that AB = BA = Identity matrix, then B is called the inverse matrix of A.
Not every matrix A has an inverse,if the inverse does exist, A is called regular/invertible/nonsingular matrix.
Liner equation { 2 x + y = 1 x − y = − 1 ⇔ { 2 x 1 + x 2 = 1 x 1 − x 2 = − 1 \begin{cases} 2x+y=1\\x-y=-1 \end{cases} \Leftrightarrow \begin{cases} 2x_1+x_2=1\\x_1-x_2=-1 \end{cases} { 2 x + y = 1 x − y = − 1 ⇔ { 2 x 1 + x 2 = 1 x 1 − x 2 = − 1 ⇔ [ 2 1 1 − 1 ] [ x 1 x 2 ] = [ 1 − 1 ] ⇔ x 1 [ 2 1 ] + x 2 [ 1 − 1 ] = [ 1 − 1 ] \Leftrightarrow \begin{bmatrix} 2&1\\1&-1 \end{bmatrix} \begin{bmatrix} x_1\\x_2 \end{bmatrix} = \begin{bmatrix} 1\\-1 \end{bmatrix} \Leftrightarrow x_1 \begin{bmatrix} 2\\1 \end{bmatrix} + x_2 \begin{bmatrix} 1\\-1 \end{bmatrix} =\begin{bmatrix} 1\\-1 \end{bmatrix} ⇔ [ 2 1 1 − 1 ] [ x 1 x 2 ] = [ 1 − 1 ] ⇔ x 1 [ 2 1 ] + x 2 [ 1 − 1 ] = [ 1 − 1 ] General formula
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m ⇔ A x = B \begin{cases} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n =b_1\\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n =b_2\\ \cdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n =b_m \end{cases} \Leftrightarrow Ax= B ⎩ ⎨ ⎧ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a mn x n = b m ⇔ A x = B ⇔ = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 . . . a m n ] [ x 1 x 2 ⋮ x n ] = [ b 1 b 2 ⋮ b m ] \Leftrightarrow =\begin{bmatrix} a_{11}&a_{12}&...&a_{1n}\\ a_{21}&a_{22}&...&a_{2n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{m1}&a_{m2}&...&a_{mn} \end{bmatrix} \begin{bmatrix} x_1\\x_2\\ \vdots\\x_n \end{bmatrix} = \begin{bmatrix} b_1\\b_2\\ \vdots \\ b_m \end{bmatrix} ⇔= ⎣ ⎡ a 11 a 21 ⋮ a m 1 a 12 a 22 ⋮ a m 2 ... ... ⋱ ... a 1 n a 2 n ⋮ a mn ⎦ ⎤ ⎣ ⎡ x 1 x 2 ⋮ x n ⎦ ⎤ = ⎣ ⎡ b 1 b 2 ⋮ b m ⎦ ⎤ Example solving Linear Equations using Matrix Method
Illustration
{ x 1 + 8 x 3 − 4 x 4 = 42 x 2 + 2 x 3 + 12 x 4 = 8 \begin{cases} x_1+8x_3-4x_4=42\\ x_2+2x_3+12x_4=8\\ \end{cases} \\ { x 1 + 8 x 3 − 4 x 4 = 42 x 2 + 2 x 3 + 12 x 4 = 8 Solution
[ 1 0 8 − 4 0 1 2 12 ] [ x 1 x 2 x 3 x 4 ] = [ 42 8 ] \begin{bmatrix} 1&0&8&-4\\0&1&2&12 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\x_4 \end{bmatrix}= \begin{bmatrix} 42\\8 \end{bmatrix} [ 1 0 0 1 8 2 − 4 12 ] ⎣ ⎡ x 1 x 2 x 3 x 4 ⎦ ⎤ = [ 42 8 ] ⇔ x 1 [ 1 0 ] + x 2 [ 0 1 ] + x 3 [ 8 2 ] + x 4 [ − 4 12 ] = [ 42 8 ] \Leftrightarrow x_1 \begin{bmatrix}1\\0\end{bmatrix} + x_2 \begin{bmatrix}0\\1\end{bmatrix} + x_3 \begin{bmatrix}8\\2\end{bmatrix} + x_4 \begin{bmatrix}-4\\12\end{bmatrix} = \begin{bmatrix} 42\\8 \end{bmatrix} ⇔ x 1 [ 1 0 ] + x 2 [ 0 1 ] + x 3 [ 8 2 ] + x 4 [ − 4 12 ] = [ 42 8 ] ⇔ ∑ i = 1 4 x i c i = b \Leftrightarrow \sum^4_{i=1} x_ic_i = b ⇔ i = 1 ∑ 4 x i c i = b with c is columns
We can see that x ∗ = [ 42 , 8 , 0 , 0 ] T ( ⇒ A x ∗ = b ) ( 1 ) x^*=[42,8,0,0]^T(\Rightarrow Ax^*=b)(1) x ∗ = [ 42 , 8 , 0 , 0 ] T ( ⇒ A x ∗ = b ) ( 1 )
So how do we find the remaining solutions of the equation?
We have:
c 3 = [ 8 2 ] = 8 c 1 + 2 c 2 ⇒ c 3 − 8 c 1 − 2 c 2 = 0 c_3 = \begin{bmatrix} 8\\2 \end{bmatrix} = 8c_1 + 2c_2 \Rightarrow c_3-8c_1-2c_2 = 0 c 3 = [ 8 2 ] = 8 c 1 + 2 c 2 ⇒ c 3 − 8 c 1 − 2 c 2 = 0 ⇔ [ c 1 c 2 c 3 c 4 ] [ − 8 − 2 1 0 ] = 0 ⇔ A λ 1 [ − 8 − 2 1 0 ] = 0 , λ 1 ∈ R \Leftrightarrow \begin{bmatrix} c_1&c_2&c_3&c_4 \end{bmatrix} \begin{bmatrix}-8\\-2\\1\\0\end{bmatrix} = 0 \Leftrightarrow \begin{equation} A \lambda_1 \begin{bmatrix}-8\\-2\\1\\0 \end{bmatrix}=0 , \lambda_1 \in R \end{equation} ⇔ [ c 1 c 2 c 3 c 4 ] ⎣ ⎡ − 8 − 2 1 0 ⎦ ⎤ = 0 ⇔ A λ 1 ⎣ ⎡ − 8 − 2 1 0 ⎦ ⎤ = 0 , λ 1 ∈ R Similar:
A λ 2 [ 4 − 12 0 1 ] = 0 , λ 2 ∈ R \begin{equation} A \lambda_2 \begin{bmatrix}4\\-12\\0\\1 \end{bmatrix}=0 , \lambda_2 \in R \end{equation} A λ 2 ⎣ ⎡ 4 − 12 0 1 ⎦ ⎤ = 0 , λ 2 ∈ R From ( 1 ) , ( 2 ) and ( 3 ) (1), (2) \text{and } (3) ( 1 ) , ( 2 ) and ( 3 )
A ( x ∗ + λ 1 [ 8 − 2 1 0 ] + λ 2 [ 4 − 12 0 1 ] ) = b , λ 1 λ 2 ∈ R A(x^* +\lambda_1 \begin{bmatrix}8\\-2\\1\\0 \end{bmatrix} + \lambda_2 \begin{bmatrix}4\\-12\\0\\1\end{bmatrix}) =b, \lambda_1 \lambda_2 \in R A ( x ∗ + λ 1 ⎣ ⎡ 8 − 2 1 0 ⎦ ⎤ + λ 2 ⎣ ⎡ 4 − 12 0 1 ⎦ ⎤ ) = b , λ 1 λ 2 ∈ R Finally: x = [ 42 8 0 0 ] + λ 1 [ 8 − 2 1 0 ] + λ 2 [ 4 − 12 0 1 ] , λ 1 λ 2 ∈ R x=\begin{bmatrix}42\\8\\0\\0\end{bmatrix} + \lambda_1\begin{bmatrix}8\\-2\\1\\0\end{bmatrix} + \lambda_2 \begin{bmatrix}4\\-12\\0\\1\end{bmatrix}, \lambda_1 \lambda_2 \in R x = ⎣ ⎡ 42 8 0 0 ⎦ ⎤ + λ 1 ⎣ ⎡ 8 − 2 1 0 ⎦ ⎤ + λ 2 ⎣ ⎡ 4 − 12 0 1 ⎦ ⎤ , λ 1 λ 2 ∈ R
How to solve system of equations:
∙ \bullet ∙ A x = b Ax=b A x = b
∙ \bullet ∙ A x = 0 Ax=0 A x = 0
∙ \bullet ∙
A matrix is in row-echelon form if:
∙ \bullet ∙
∙ \bullet ∙
Remark : The variables corresponding to the pivots in the row-echelon
form are called basic variables and the other basic variable variables are
free variables.
⌈ 1 − 2 1 − 1 1 0 0 1 − 1 3 0 0 0 1 − 2 0 0 0 0 0 ∣ ∣ 0 − 2 1 a + 1 ⌉ \left\lceil \begin{matrix} 1&-2&1&-1&1 \\ 0&0&1&-1&3 \\0&0&0&1&-2 \\0&0&0&0&0 \end{matrix} \right\rvert \left\rvert \begin{matrix} 0\\-2\\1\\ a+1 \end{matrix} \right\rceil ⎢ ⎡ 1 0 0 0 − 2 0 0 0 1 1 0 0 − 1 − 1 1 0 1 3 − 2 0 ∣ ∣ ∣ ∣ 0 − 2 1 a + 1 ⎥ ⎤ x 1 , x 3 , x 4 x_1,x_3,x_4 x 1 , x 3 , x 4 x 2 , x 5 x_2, x_5 x 2 , x 5
An equation system is in reduced reduced row-echelon form if:
∙ \bullet ∙
∙ \bullet ∙
∙ \bullet ∙
Gaussian elimination is an algorithm that elimination performs elementary
transformations to bring a system of linear equations into reduced
row-echelon form.
Exercise Ex1: Compute the following matrix products, if possible:
(a) A = [ 1 2 3 ] [ 1 2 3 ] A=\begin{bmatrix}1\\2\\3 \end{bmatrix} \begin{bmatrix}1&2&3 \end{bmatrix} A = ⎣ ⎡ 1 2 3 ⎦ ⎤ [ 1 2 3 ]
A = [ 1 × 1 2 × 2 3 × 3 ] = [ 1 4 9 ] A = \begin{bmatrix}1\times1 & 2\times 2 & 3\times3 \end{bmatrix} = \begin{bmatrix} 1&4&9 \end{bmatrix} A = [ 1 × 1 2 × 2 3 × 3 ] = [ 1 4 9 ] (b) B = [ 1 2 3 ] [ 1 2 3 ] B=\begin{bmatrix}1&2&3 \end{bmatrix} \begin{bmatrix}1\\2\\3 \end{bmatrix} B = [ 1 2 3 ] ⎣ ⎡ 1 2 3 ⎦ ⎤
B = [ 1 × 1 + 2 × 2 + 3 × 3 ] = 14 B = [1\times1 + 2\times 2 + 3\times3] = 14 B = [ 1 × 1 + 2 × 2 + 3 × 3 ] = 14 (c) C = [ 1 2 4 5 7 8 ] [ 1 1 0 0 1 1 1 0 1 ] C=\begin{bmatrix}1&2\\4&5\\7&8 \end{bmatrix} \begin{bmatrix}1&1&0\\0&1&1\\1&0&1 \end{bmatrix} C = ⎣ ⎡ 1 4 7 2 5 8 ⎦ ⎤ ⎣ ⎡ 1 0 1 1 1 0 0 1 1 ⎦ ⎤
We cannot solve that calculation, because the number of elements in the row is not equal to the number of elements in the column
(d) D = [ 1 1 0 0 1 1 1 0 1 ] [ 1 2 3 4 5 6 7 8 9 ] D=\begin{bmatrix}1&1&0\\0&1&1\\1&0&1 \end{bmatrix} \begin{bmatrix}1&2&3\\4&5&6\\7&8&9\end{bmatrix} D = ⎣ ⎡ 1 0 1 1 1 0 0 1 1 ⎦ ⎤ ⎣ ⎡ 1 4 7 2 5 8 3 6 9 ⎦ ⎤
D = [ 5 7 9 11 13 15 8 10 12 ] D = \begin{bmatrix} 5&7&9\\11&13&15 \\ 8&10&12 \end{bmatrix} D = ⎣ ⎡ 5 11 8 7 13 10 9 15 12 ⎦ ⎤ (e) E = [ 1 2 1 2 4 1 − 1 − 4 ] [ 0 3 1 − 1 2 1 5 2 ] E=\begin{bmatrix} 1&2&1&2\\4&1&-1&-4 \end{bmatrix} \begin{bmatrix} 0&3\\1&-1\\2&1\\5&2\end{bmatrix} E = [ 1 4 2 1 1 − 1 2 − 4 ] ⎣ ⎡ 0 1 2 5 3 − 1 1 2 ⎦ ⎤
E = [ 14 6 − 21 2 ] E = \begin{bmatrix} 14&6\\-21&2 \end{bmatrix} E = [ 14 − 21 6 2 ] Ex2: Using Gaussian elimination, find the set S S S A x = b Ax = b A x = b A A A b b b
(a) A = [ 1 1 − 1 0 2 1 1 1 − 4 ] [ 1 1 0 ] A=\begin{bmatrix} 1&1&-1\\0&2&1\\1&1&-4 \end{bmatrix} \begin{bmatrix}1\\1\\0 \end{bmatrix} A = ⎣ ⎡ 1 0 1 1 2 1 − 1 1 − 4 ⎦ ⎤ ⎣ ⎡ 1 1 0 ⎦ ⎤
We have:
⌈ 1 1 − 1 0 2 1 1 1 − 4 ∣ ∣ 1 1 0 ⌉ = ⌈ 1 1 − 1 1 1 − 4 0 2 1 ∣ ∣ 1 0 0 ⌉ = ⌈ 1 1 − 1 0 0 3 0 2 1 ∣ ∣ 1 1 1 ⌉ \left\lceil \begin{matrix} 1&1&-1\\0&2&1\\1&1&-4 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\1\\0 \end{matrix} \right\rceil = \left\lceil \begin{matrix} 1&1&-1\\1&1&-4\\0&2&1 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\0\\0 \end{matrix} \right\rceil = \left\lceil \begin{matrix} 1&1&-1\\0&0&3\\0&2&1 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\1\\1 \end{matrix} \right\rceil ⎢ ⎡ 1 0 1 1 2 1 − 1 1 − 4 ∣ ∣ ∣ ∣ 1 1 0 ⎥ ⎤ = ⎢ ⎡ 1 1 0 1 1 2 − 1 − 4 1 ∣ ∣ ∣ ∣ 1 0 0 ⎥ ⎤ = ⎢ ⎡ 1 0 0 1 0 2 − 1 3 1 ∣ ∣ ∣ ∣ 1 1 1 ⎥ ⎤ ⇔ { x + y − z = 1 3 z = 1 2 y + z = 1 ⇔ { x = 1 y = 1 3 z = 1 3 \Leftrightarrow \begin{cases} x+y-z=1\\3z=1\\2y+z=1 \end{cases} \Leftrightarrow \begin{cases} x=1\\y=\frac{1}{3}\\z=\frac{1}{3} \end{cases} ⇔ ⎩ ⎨ ⎧ x + y − z = 1 3 z = 1 2 y + z = 1 ⇔ ⎩ ⎨ ⎧ x = 1 y = 3 1 z = 3 1 (b) B = [ 1 1 − 1 − 1 2 5 − 7 − 5 2 − 1 1 3 5 2 − 4 2 ] [ 1 − 2 4 6 ] B=\begin{bmatrix} 1&1&-1&-1\\2&5&-7&-5\\2&-1&1&3\\5&2&-4&2 \end{bmatrix} \begin{bmatrix}1\\-2\\4\\6 \end{bmatrix} B = ⎣ ⎡ 1 2 2 5 1 5 − 1 2 − 1 − 7 1 − 4 − 1 − 5 3 2 ⎦ ⎤ ⎣ ⎡ 1 − 2 4 6 ⎦ ⎤
We have:
⌈ 1 1 − 1 − 1 2 5 − 7 − 5 2 − 1 1 3 5 2 − 4 2 ∣ ∣ 1 − 2 4 6 ⌉ = ⌈ 1 1 − 1 − 1 0 − 3 5 3 0 − 3 3 5 0 − 3 1 7 ∣ ∣ 1 4 2 1 ⌉ \left\lceil \begin{matrix} 1&1&-1&-1\\2&5&-7&-5\\2&-1&1&3\\5&2&-4&2 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\-2\\4\\6 \end{matrix} \right\rceil = \left\lceil \begin{matrix} 1&1&-1&-1\\0&-3&5&3\\0&-3&3&5\\0&-3&1&7 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\4\\2\\1 \end{matrix} \right\rceil ⎢ ⎡ 1 2 2 5 1 5 − 1 2 − 1 − 7 1 − 4 − 1 − 5 3 2 ∣ ∣ ∣ ∣ 1 − 2 4 6 ⎥ ⎤ = ⎢ ⎡ 1 0 0 0 1 − 3 − 3 − 3 − 1 5 3 1 − 1 3 5 7 ∣ ∣ ∣ ∣ 1 4 2 1 ⎥ ⎤ = ⌈ 1 1 − 1 − 1 0 − 3 5 3 0 0 2 − 2 0 0 4 4 ∣ ∣ 1 4 2 3 ⌉ = ⌈ 1 1 − 1 − 1 0 − 3 5 3 0 0 1 − 1 0 0 1 1 ∣ ∣ 1 4 1 3 4 ⌉ = ⌈ 1 1 − 1 − 1 0 − 3 5 3 0 0 1 − 1 0 0 0 − 2 ∣ ∣ 1 4 1 1 4 ⌉ = \left\lceil \begin{matrix} 1&1&-1&-1\\0&-3&5&3\\0&0&2&-2\\0&0&4&4 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\4\\2\\3 \end{matrix} \right\rceil = \left\lceil \begin{matrix} 1&1&-1&-1\\0&-3&5&3\\0&0&1&-1\\0&0&1&1 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\4\\1\\\frac{3}{4} \end{matrix} \right\rceil = \left\lceil \begin{matrix} 1&1&-1&-1\\0&-3&5&3\\0&0&1&-1\\0&0&0&-2 \end{matrix} \right\rvert \left\rvert \begin{matrix} 1\\4\\1\\\frac{1}{4} \end{matrix} \right\rceil = ⎢ ⎡ 1 0 0 0 1 − 3 0 0 − 1 5 2 4 − 1 3 − 2 4 ∣ ∣ ∣ ∣ 1 4 2 3 ⎥ ⎤ = ⎢ ⎡ 1 0 0 0 1 − 3 0 0 − 1 5 1 1 − 1 3 − 1 1 ∣ ∣ ∣ ∣ 1 4 1 4 3 ⎥ ⎤ = ⎢ ⎡ 1 0 0 0 1 − 3 0 0 − 1 5 1 0 − 1 3 − 1 − 2 ∣ ∣ ∣ ∣ 1 4 1 4 1 ⎥ ⎤ ⇒ { x + y + z + m = 1 − 3 y + 5 z + 3 m = 4 z − m = 1 − 2 m = 1 4 ⇒ { x = 3 2 y = 5 4 z = 7 8 m = − 1 8 \Rightarrow \begin{cases} x+y+z+m =1 \\-3y+5z+3m=4\\z-m=1\\-2m=\frac{1}{4} \end{cases} \Rightarrow \begin{cases} x=\frac{3}{2} \\ y=\frac{5}{4}\\ z= \frac{7}{8}\\m=\frac{-1}{8} \end{cases} ⇒ ⎩ ⎨ ⎧ x + y + z + m = 1 − 3 y + 5 z + 3 m = 4 z − m = 1 − 2 m = 4 1 ⇒ ⎩ ⎨ ⎧ x = 2 3 y = 4 5 z = 8 7 m = 8 − 1 (c) C = [ 2 1 1 − 1 2 1 ] [ 3 6 ] C=\begin{bmatrix} 2&1&1\\-1&2&1 \end{bmatrix} \begin{bmatrix}3\\6 \end{bmatrix} C = [ 2 − 1 1 2 1 1 ] [ 3 6 ]
(d) C = [ 2 1 − 1 2 1 1 ] [ 3 6 − 1 ] C=\begin{bmatrix}2&1\\-1&2\\1&1 \end{bmatrix} \begin{bmatrix}3\\6\\-1 \end{bmatrix} C = ⎣ ⎡ 2 − 1 1 1 2 1 ⎦ ⎤ ⎣ ⎡ 3 6 − 1 ⎦ ⎤
Ex3: Determine the inverses of the following matrices if possible:
(a) A = [ 2 0 0 0 − 1 0 0 0 6 ] A=\begin{bmatrix} 2&0&0\\0&-1&0\\0&0&6 \end{bmatrix} A = ⎣ ⎡ 2 0 0 0 − 1 0 0 0 6 ⎦ ⎤
We have: A A − 1 = I AA^{-1} =I A A − 1 = I
[ 2 0 0 0 − 1 0 0 0 6 ] [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] = [ 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix} 2&0&0\\0&-1&0\\0&0&6\end{bmatrix} \begin{bmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix} = \begin{bmatrix} 1&0&0\\0&1&0\\0&0&1 \end{bmatrix} ⎣ ⎡ 2 0 0 0 − 1 0 0 0 6 ⎦ ⎤ ⎣ ⎡ a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 ⎦ ⎤ = ⎣ ⎡ 1 0 0 0 1 0 0 0 1 ⎦ ⎤ ⇔ [ − 2 a 11 2 a 12 2 a 13 − a 21 − a 22 − a 23 6 a 31 6 a 32 6 a 33 ] = [ 1 0 0 0 1 0 0 0 1 ] \Leftrightarrow \begin{bmatrix} -2a_{11}&2a_{12}&2a_{13}\\-a_{21}&-a_{22}&-a_{23}\\6a_{31}&6a_{32}&6a_{33}\end{bmatrix} = \begin{bmatrix} 1&0&0\\0&1&0\\0&0&1 \end{bmatrix} ⇔ ⎣ ⎡ − 2 a 11 − a 21 6 a 31 2 a 12 − a 22 6 a 32 2 a 13 − a 23 6 a 33 ⎦ ⎤ = ⎣ ⎡ 1 0 0 0 1 0 0 0 1 ⎦ ⎤ ⇔ A − 1 = [ 1 2 0 0 0 − 1 0 0 0 1 6 ] \Leftrightarrow A^{-1} = \begin{bmatrix} \frac{1}{2}&0&0\\0&-1&0\\0&0&\frac{1}{6} \end{bmatrix} ⇔ A − 1 = ⎣ ⎡ 2 1 0 0 0 − 1 0 0 0 6 1 ⎦ ⎤ (b) B = [ 4 1 3 1 ] B=\begin{bmatrix} 4&1\\3&1 \end{bmatrix} B = [ 4 3 1 1 ]
We have: B B − 1 = I BB^{-1} =I B B − 1 = I
[ 4 1 3 1 ] [ a 11 a 12 a 21 a 22 ] = [ 1 0 0 1 ] \begin{bmatrix} 4&1\\3&1 \end{bmatrix} \begin{bmatrix} a_{11}&a_{12}\\a_{21}&a_{22} \end{bmatrix} = \begin{bmatrix} 1&0\\0&1\end{bmatrix} [ 4 3 1 1 ] [ a 11 a 21 a 12 a 22 ] = [ 1 0 0 1 ] ⇔ [ 4 a 11 + a 21 4 a 12 + a 22 3 a 11 + a 21 3 a 12 + a 22 ] = [ 1 0 0 1 ] \Leftrightarrow \begin{bmatrix} 4a_{11} + a_{21}&4a_{12}+a_{22}\\3a_{11}+a_{21}&3a_{12}+a_{22} \end{bmatrix} = \begin{bmatrix} 1&0\\0&1\end{bmatrix} ⇔ [ 4 a 11 + a 21 3 a 11 + a 21 4 a 12 + a 22 3 a 12 + a 22 ] = [ 1 0 0 1 ] ⇒ B − 1 = [ 1 − 1 − 3 4 ] \Rightarrow B^{-1} = \begin{bmatrix} 1&-1\\-3&4 \end{bmatrix} ⇒ B − 1 = [ 1 − 3 − 1 4 ] Linear Independent Group Consider a set G \mathcal{G} G ⊗ \otimes ⊗ G × G → G \mathcal{G} \times \mathcal{G} \rightarrow \mathcal{G} G × G → G G \mathcal{G} G G : = ( G , ⊗ ) \mathcal{G} := (\mathcal{G},\otimes) G := ( G , ⊗ )
∙ ∀ x , y ∈ G , x ⊗ y ∈ G \bullet \forall x, y \in \mathcal{G} , x \otimes y \in \mathcal{G} ∙ ∀ x , y ∈ G , x ⊗ y ∈ G
∙ ∀ x , y , z ∈ G , ( x ⊗ y ) ⊗ z = x ⊗ ( y ⊗ z ) \bullet \forall x,y,z \in \mathcal{G}, (x\otimes y) \otimes z = x \otimes (y \otimes z) ∙ ∀ x , y , z ∈ G , ( x ⊗ y ) ⊗ z = x ⊗ ( y ⊗ z )
∙ ∃ e ∈ G , ∀ x ∈ G : x ⊗ e = e ⊗ x = x \bullet \exists e \in \mathcal{G} , \forall x \in \mathcal{G}: x\otimes e = e\otimes x = x ∙ ∃ e ∈ G , ∀ x ∈ G : x ⊗ e = e ⊗ x = x
∙ ∀ x ∈ G , ∃ y ∈ G : x ⊗ y = y ⊗ x = e \bullet \forall x \in \mathcal{G}, \exists y \in \mathcal{G}: x \otimes y = y \otimes x =e ∙ ∀ x ∈ G , ∃ y ∈ G : x ⊗ y = y ⊗ x = e
If additionally, ∀ x , y ∈ G : x ⊗ y = y ⊗ x \forall x,y \in \mathcal{G}: x \otimes y = y \otimes x ∀ x , y ∈ G : x ⊗ y = y ⊗ x G = ( G , ⊗ ) G=(\mathcal{G}, \otimes) G = ( G , ⊗ ) Abelian group
Example
With ( R , + ) (R,+) ( R , + )
∙ ∀ x , y ∈ R → x + y ∈ R \bullet \forall x,y \in R \rightarrow x+y \in R ∙ ∀ x , y ∈ R → x + y ∈ R
∙ ∀ x , y , z ∈ R → ( x − y ) + z = x + ( y + z ) \bullet \forall x,y,z \in R \rightarrow (x-y)+z = x+(y+z) ∙ ∀ x , y , z ∈ R → ( x − y ) + z = x + ( y + z )
∙ ∀ x ∈ R , ∃ e = 0 : x + 0 = 0 + x \bullet \forall x \in R , \exists e=0: x+0 =0+x ∙ ∀ x ∈ R , ∃ e = 0 : x + 0 = 0 + x
∙ ∀ x ∈ R , ∃ y = − x → x + y = 0 \bullet \forall x \in R , \exists y=-x \rightarrow x+y = 0 ∙ ∀ x ∈ R , ∃ y = − x → x + y = 0
⇒ ( R , + ) \Rightarrow (R,+) ⇒ ( R , + )
With ( Z , × ) (Z, \times) ( Z , × )
∙ ∀ x , y ∈ Z → x × y ∈ Z \bullet \forall x,y \in Z \rightarrow x\times y \in Z ∙ ∀ x , y ∈ Z → x × y ∈ Z
∙ ∀ x , y , z ∈ Z → ( x × y ) × z = x × ( y × z ) \bullet \forall x,y,z \in Z \rightarrow (x\times y)\times z = x\times (y\times z) ∙ ∀ x , y , z ∈ Z → ( x × y ) × z = x × ( y × z )
∙ ∀ x ∈ Z , ∃ e = 1 : x × 1 = 1 × x \bullet \forall x \in Z , \exists e=1: x\times 1 =1 \times x ∙ ∀ x ∈ Z , ∃ e = 1 : x × 1 = 1 × x
∙ ∀ x ∈ Z , ∃ y = 0 → x × y = y × x = 0 ≠ e \bullet \forall x \in Z , \exists y=0 \rightarrow x\times y =y\times x = 0 \neq e ∙ ∀ x ∈ Z , ∃ y = 0 → x × y = y × x = 0 = e
⇒ ( Z , × ) \Rightarrow (Z,\times) ⇒ ( Z , × )
With ( R n , . ) (R^n, .) ( R n , . )
∙ ∀ x , y ∈ R n ( v e c t o r ) → x + y ∈ R n \bullet \forall x,y \in R^n (vector) \rightarrow x + y \in R^n ∙ ∀ x , y ∈ R n ( v ec t or ) → x + y ∈ R n
∙ ∀ x , y , z ∈ R n → ( x − y ) + z = x + ( y + z ) \bullet \forall x,y,z \in R^n \rightarrow (x-y)+z = x+(y+z) ∙ ∀ x , y , z ∈ R n → ( x − y ) + z = x + ( y + z )
∙ ∀ x ∈ R n , ∃ e = [ 1 1 . . . 1 ] : x + e = e + x \bullet \forall x \in R^n , \exists e=\begin{bmatrix}1\\1\\...\\1\end{bmatrix}: x+e =e+x ∙ ∀ x ∈ R n , ∃ e = ⎣ ⎡ 1 1 ... 1 ⎦ ⎤ : x + e = e + x
∙ ∀ x ∈ R n , ∃ y = − x → x + y = 0 \bullet \forall x \in R^n , \exists y=-x \rightarrow x+y = 0 ∙ ∀ x ∈ R n , ∃ y = − x → x + y = 0
⇒ ( R n , + ) \Rightarrow (R^n,+) ⇒ ( R n , + )
With ( R n × n , × ) (R^{n\times n}, \times) ( R n × n , × )
Does not satisfy condition 4, because we have A . B = I n A.B=I_n A . B = I n
⇒ ( R n × n , × ) \Rightarrow (R^{n\times n}, \times) ⇒ ( R n × n , × )
Vector space A real-valued vector space V = ( V ; + ; × ) V=(\mathcal{V};+;\times) V = ( V ; + ; × ) V \mathcal{V} V
∙ ( V ; + ) is an Abelian group \bullet (\mathcal{V};+) \text{is an Abelian group} ∙ ( V ; + ) is an Abelian group
∙ ∀ λ , γ ∈ r , x , y ∈ V : \bullet \forall \lambda,\gamma \in r, x,y \in \mathcal{V}: ∙ ∀ λ , γ ∈ r , x , y ∈ V :
λ ( x + y ) = λ x + λ y \quad \quad \quad \lambda(x+y)= \lambda x+\lambda y λ ( x + y ) = λ x + λ y
( λ + γ ) x = λ x + γ x \quad \quad \quad (\lambda + \gamma)x= \lambda x+\gamma x ( λ + γ ) x = λ x + γ x
∙ ∀ λ , γ ∈ R , x ∈ V : λ ( γ x ) = ( λ γ ) x \bullet \forall \lambda, \gamma \in R, x \in \mathcal{V}: \lambda(\gamma x) = (\lambda \gamma)x ∙ ∀ λ , γ ∈ R , x ∈ V : λ ( γ x ) = ( λγ ) x
∙ 1 × x = x \bullet 1\times x=x ∙ 1 × x = x
The elements x ∈ V x \in \mathcal{V} x ∈ V vectors , examples: V = R n \mathcal{V} = R^n V = R n
We will denote a vector space ( V , + , . ) (\mathcal{V}, +, .) ( V , + , . )
Moreover, we will use the notation x ∈ V x\in V x ∈ V V \mathcal{V} V
Default, the vectors are column vectors:
x = [ x 1 x 2 . . x n ] ∈ R n × 1 ⇒ x T = [ x 1 x 2 . . . x n ] ∈ R 1 × n x=\begin{bmatrix}x_1\\x_2\\..\\ x_n\end{bmatrix} \in R^{n\times 1} \Rightarrow x^T = \begin{bmatrix} x_1 & x_2 & ... & x_n \end{bmatrix} \in R^{1\times n } x = ⎣ ⎡ x 1 x 2 .. x n ⎦ ⎤ ∈ R n × 1 ⇒ x T = [ x 1 x 2 ... x n ] ∈ R 1 × n Vector subspaces